本文介绍了强化学习问题中最简单基本的算法——动态规划(Dynamic Programming),介绍了贝尔曼方程在该算法中的应用。
DP的基本概念
动态规划(dynamic programming)是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法。20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时,提出了著名的最优化原理(principle of optimality),把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。1957年出版了他的名著《Dynamic Programming》,这是该领域的第一本著作。——百度百科)
动态规划-DP算法指的不是单一一个算法,而是一系列可以在给定满足MDP的完全可知环境模型中计算出最优策略的算法。
DP的特点:
- Model-Based
- Value-Based
- Off-Policy(这个比较牵强,因为DP不涉及采样、预测,完全靠planning)
DP具有很重要的理论基础作用,但是在现在的强化学习问题中,DP并不常使用,主要原因有二:
- 需要完全可知的模型,状态空间、动作空间离散,状态转移、奖励函数可知且确定
- 计算量很大(每次更新都需要完全规划所有可能性)
在一些表格型的问题中,如完全可知的迷宫,可以使用DP,但是要解决人类现实世界极其复杂的问题、任务,DP可能就有些力不从心啦。
其实,所有的强化学习算法都可以被认为是在不完全可知的环境中使用少量计算得到如DP效果一样的策略(最优策略)。
算法
先回顾一下之前提到的贝尔曼方程。
贝尔曼期望方程:
贝尔曼最优方程:
为什么要再次提到贝尔曼方程呢?因为动态规划算法中的策略迭代、值迭代就是将贝尔曼方程给结合了起来。
回顾一下在价值与贝尔曼方差最后的例子中迭代计算$V(S)$和$Q(S,A)$,遍历所有$Q(S,A)$以计算$V(S)$,再遍历所有$V(S)$以计算$Q(S,A)$。在一个简单的场景下循环迭代至收敛就需要很大的计算量,如果在复杂场景中(还是完全可知的)迭代计算可想有多费时费力,动态规划DP下的Policy Iteration和Value Iteration减轻了计算的负担,同时又不影响收敛性。
引用《Reinfocement Learning : An Introduction》中的一个网格世界的例子:
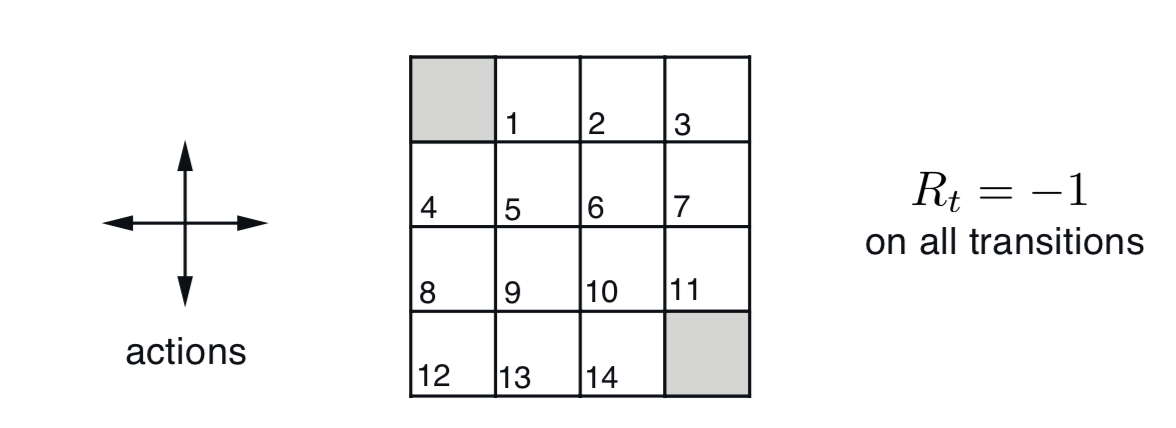
在这个例子中,有1-14个非终态以及两个终态(左上角、右下角),动作空间为上下左右四种,在边缘位置的状态,例如$S=1$,可选的动作只有左右下三种,且等概率选择每种动作,每进行一次移动,就给予-1的奖励值。智能体需要尽快的到达网格世界的出口-终态,以获得尽量少的负奖励(即累计奖励最大)。
如果按照先遍历所有$Q(S,A)$以计算$V(S)$,再遍历所有$V(S)$以计算$Q(S,A)$的方式计算,值函数的表格将会如下图所示:
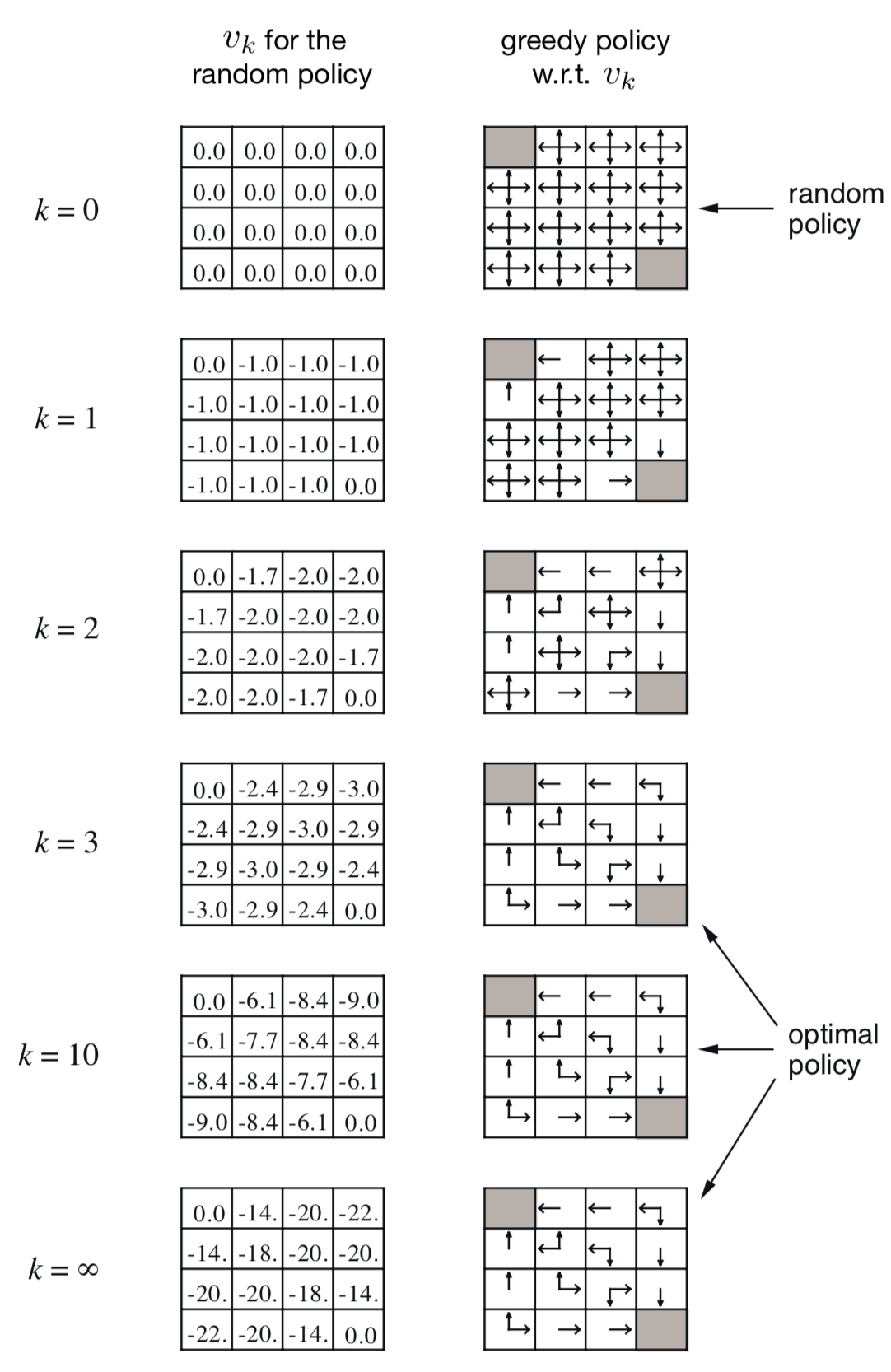
左边展示的是进行$k$次迭代,使值函数表格可以收敛,右边表示在每次迭代中,取$a=argmax_{a}q(s,a)$的策略。
可以发现,这样迭代$V(S)$至收敛有两个浪费算力的地方:
- 选择动作的概率完全按照环境设置,导致计算状态$s$的值函数时,最差的动作$a$所带来的影响也被计算在其中,但其实真正执行的时候,永远不会执行该动作。
- $k=3$与$k=10$时的策略表示一样,也就意味着,不必等到$V(S)$迭代至完全收敛就有可能可以获得最优策略,那么后续迭代完全没有用处,造成了资源浪费。
策略迭代、值迭代的思想都是贪心策略,但策略迭代针对问题1通过剪裁可选动作的方式进行了优化,值迭代针对问题2通过取最大动作值函数的方式进行了优化。
策略迭代 Policy Iteration
动作是通过策略产生的,因此势必需要对初始策略(GridWorld中的完全随机策略)进行替换,以达到更改动作选取概率的目的。
既然要在不同的阶段更改动作选择的概率,那么要进行多次策略的更改,随之而来的问题就是:
- 值函数迭代更新到什么情况下时,开始更新策略
- 如何更新策略?
针对第一个问题,我们使用策略评估Policy Evaluation的方式来解决,针对第二个问题,我们使用策略提升Policy Improvation的方式来解决,最终当新策略与旧策略相同时,终止迭代,得到最优策略。
伪代码

策略评估 Policy Evaluation
问题:值函数迭代更新到什么情况下时,开始更新策略
答:设置更新幅度阈值$\theta$,当sweep(横扫)一遍状态空间计算$V(S)$时,与上次更新时的$V(S)$相比较,如果最大的更新幅度小于阈值$\theta$,即$\Delta \lt \theta$,则认为策略评估已经完成,开始进行策略更新
特点:使用了贝尔曼期望方程-$v_{\pi}(s)$
注:策略评估指的不是评估一个策略的好坏,而是在当前策略下评估所有的状态值,使状态值表格近似收敛。
策略提升 Policy Improvement
问题:如何更新策略?
答:根据策略评估步骤得到的值函数$V(S)$,计算$Q(S,A)$表格,选取每个状态下使动作值函数最大的动作作为新的动作集,每个动作的选择概率相同,接着进行策略评估。
特点:使用了贝尔曼期望方程-$q_{\pi}(s,a)$
值迭代 Value Iteration
策略迭代的一个缺点是在得到最优策略$\pi_{\ast}$之前,需要多次更新策略,每次更新策略都会引起可选取动作的改变,这会引起在更新完策略后的前几次策略评估中值函数偏差比较大,导致在策略评估过程中需要花费大量的迭代来减小更新幅度$\Delta$,因此需要多次sweep(横扫)$V(S)$来迭代计算。
值迭代的思想是:能不能通过早停的方式,在不更改策略的情况下,直接一次得到最优策略?
值迭代运用了策略评估、策略迭代的思想,并将它们融合在一起,即不更新策略,直接选择动作值函数$q(s,a)$最大的动作作为状态值$v(s)$,直接迭代出近似最优(早停,$\Delta \lt \theta$即可)状态价值函数$V_{\ast}(S)$,使用贪心策略进而得到最优策略$\pi_{\ast}$。
特点:使用了贝尔曼最优方程-$v_{\ast}(s),q_{\ast}(s,a)$。
伪代码

PI与VI的比较
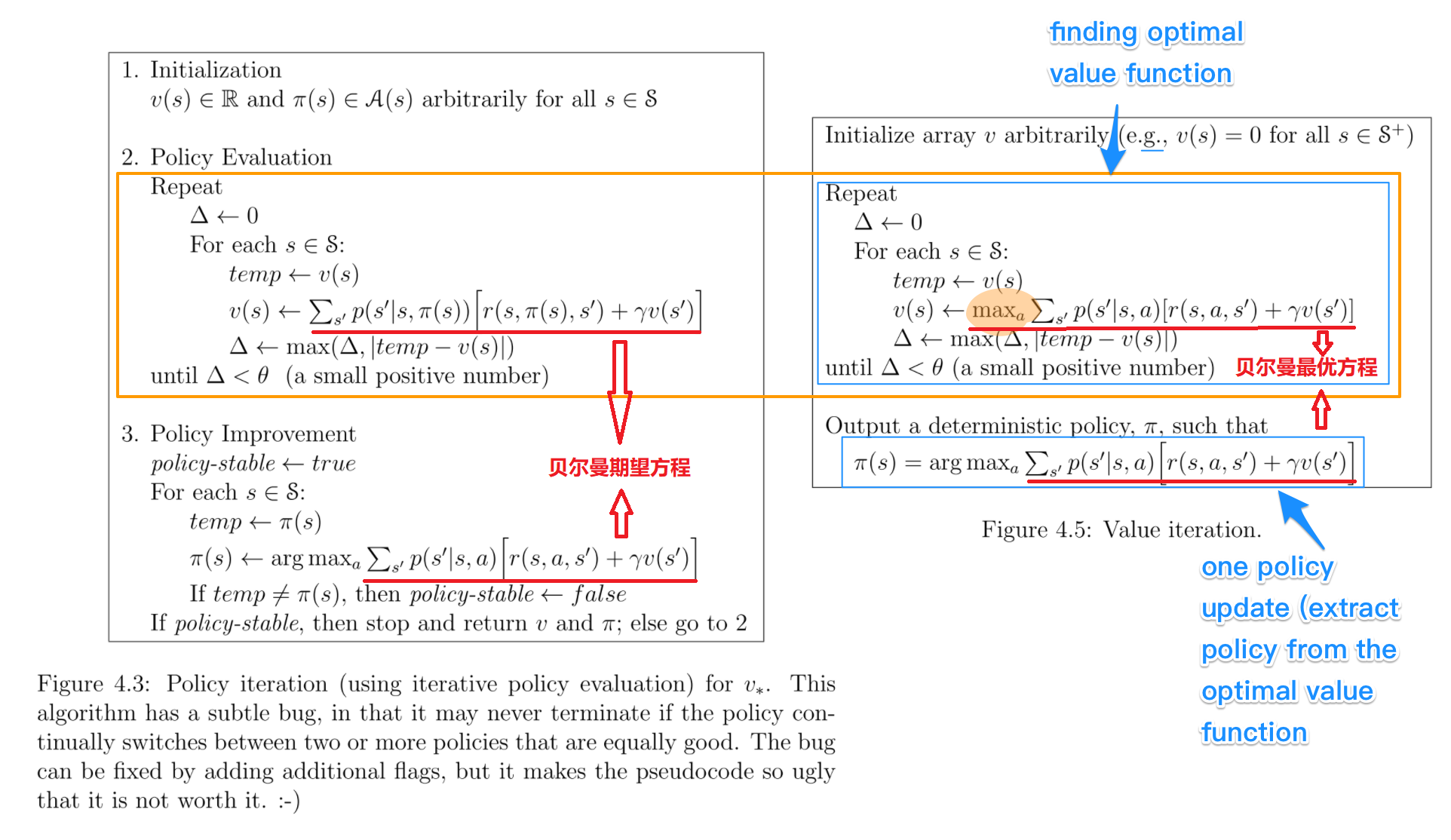
相同点:
- 在$0 \leq \gamma \lt 1$,有限MDPs环境中,两种方式都可以收敛到最优策略$\pi_{\ast}$
- 都使用了贝尔曼方程进行状态值函数的迭代
不同点:
- 收敛方式
- 策略迭代PI包括策略评估Policy Evaluation和策略提升Policy Improvement,这两部循环迭代至策略收敛
- 值迭代VI包括找到最优状态值函数和一步提取策略,这两步不需要循环迭代,而是根据最优值函数直接得到最优策略
- 动作改变方式
- 策略迭代PI获得新策略$\pi_{new}$后,更改每个状态的可选动作集,多次横扫(遍历)$V(S)$
- 值迭代VI过程中不产生策略,不更改每个状态的可选动作集,但是只取每个状态下动作值函数最大的动作作为状态值,一次横扫(遍历)$V(S)$。(这里需要解释一下,虽然循环是多次遍历,但是因为max操作,每次遍历每个状态所选取的动作不一定一样,虽然策略一直是随机策略,没有产生新策略,但是计算过程没有遍历到所有动作,可以隐含的看作是一个新策略,因此每次遍历时这个“隐策略”都会改变,所以称为一次遍历。)
- 计算方式
- 策略迭代PI使用贝尔曼期望方程
- 值迭代VI使用贝尔曼最优方程
- Policy方式
- 策略迭代PI是On-Policy
- 值迭代VI是Off-Policy
- 稳定性检查
- 策略迭代PI中更新策略时进行了策略稳定性检查,判断是否收敛
- 值迭代VI获得新策略$\pi$时没有进行策略稳定性检查
至于策略迭代PI与值迭代VI的收敛速度,通常情况下,PI的迭代次数更少,VI的运行时间更少。
What is the difference between value iteration and policy iteration?

